Principes physiques acousto-optiques - principales équations
Un signal RF appliqué à un transducteur piézo-électrique, lié à un cristal approprié, génère une onde acoustique. Celle-ci agit comme un « réseau de phase », se déplaçant à travers le cristal à la vitesse acoustique du matériau et avec une longueur d’onde acoustique dépendant de la fréquence du signal RF. Tout faisceau laser incident est diffracté par ce réseau, ce qui donne généralement un certain nombre de faisceaux diffractés.
Conditions d'interaction
Un paramètre appelé « facteur de qualité, Q », détermine le régime d’interaction. Q est donné par :
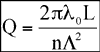
où λ0 est la longueur d’onde du faisceau laser, n est l’indice de réfraction du cristal, L est la distance parcourue par le faisceau laser à travers l’onde acoustique et ⋏ est la longueur d’onde acoustique.
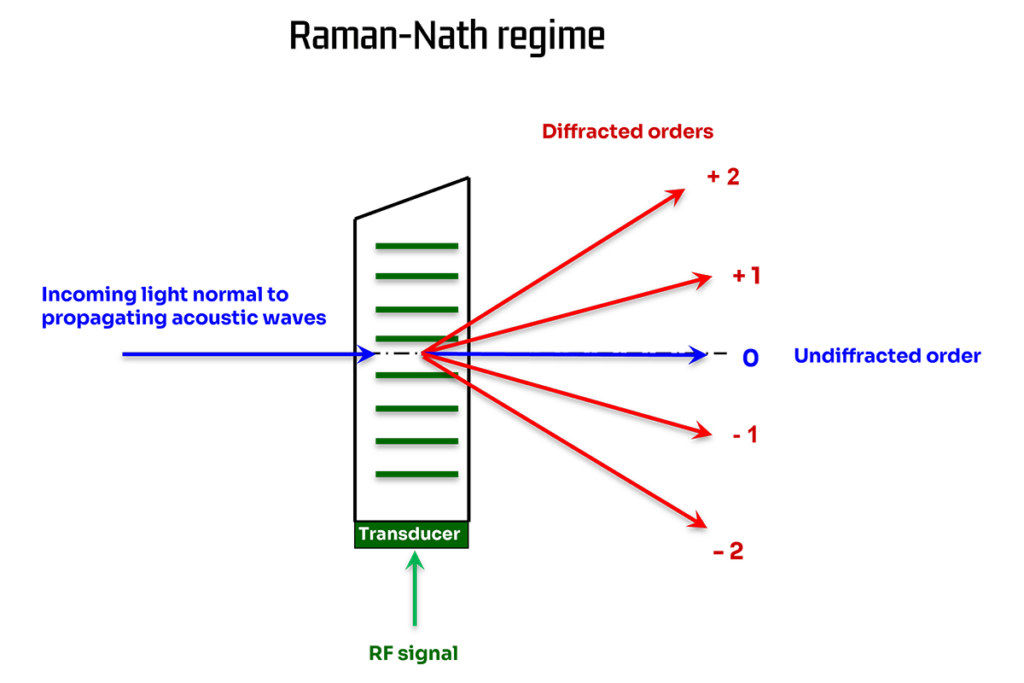
Q<<1 : C’est le régime Raman-Nath. Le faisceau laser est incident à peu près normalement au faisceau acoustique et il y a plusieurs ordres de diffraction (…-2 -1 0 1 2 3…) avec des intensités données par les fonctions de Bessel.
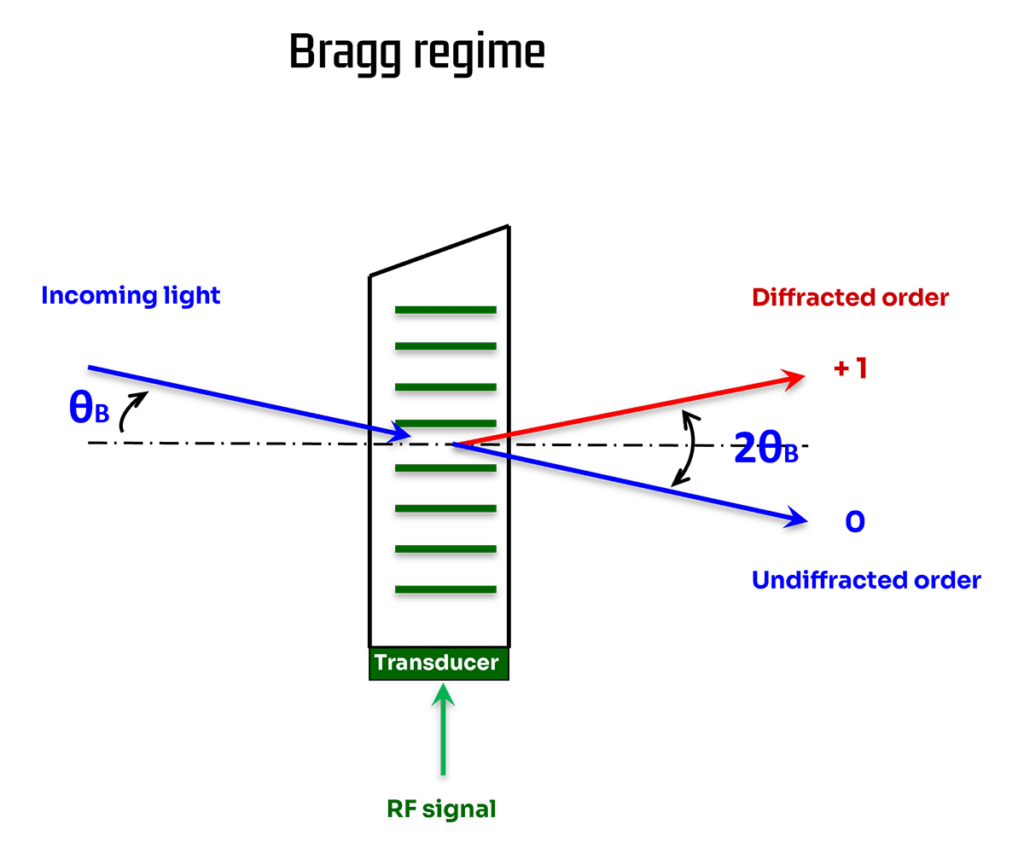
Q>>1 : C’est le régime de Bragg. À un angle d’incidence donné appelé « Angle de Bragg », un seul ordre de diffraction est produit – les autres sont annihilés par interférence destructive.
Dans la situation intermédiaire, un traitement analytique n’est pas possible et une analyse numérique doit être effectuée par ordinateur.
La plupart des dispositifs acousto-optiques fonctionnent dans le régime de Bragg, à l’exception des Mode Lockers et des Q-switches.
Constructions des vecteurs d'onde
Une interaction acousto-optique peut être décrite à l’aide de vecteurs d’onde. La conservation de la quantité de mouvement nous donne :
![]()
Ki=2πni/λ0 – vecteur d’onde du faisceau incident.
Kd=2πnd/λd – vecteur d’onde du faisceau diffracté.
K=2πF/v – vecteur d’onde de l’onde acoustique.
Ici, F est la fréquence de l’onde acoustique se déplaçant à la vitesse v. ni and nd sont les indices de réfraction des faisceaux incident et diffracté (ils ne sont pas nécessairement identiques)..
La conservation de l’énergie conduit à : Fd = Fi +/- F
Ainsi, la fréquence optique du faisceau diffracté est décalée de la fréquence de l’onde acoustique par rapport à la fréquence incidente. Ce « décalage Doppler » peut généralement être négligé puisque F >> Fd or Fi, mais il peut s’avérer très intéressant dans les applications d’hétérodynamique.
Les composants acousto-optiques utilisent toute une série de matériaux différents dans des configurations variées. Ils peuvent être décrits par des termes tels que mode longitudinal et mode de cisaillement, isotrope et anisotrope. Bien qu’ils partagent tous les principes de base de la conservation de la quantité de mouvement et de l’énergie, ces différents modes de fonctionnement ont des performances très différentes, comme nous le verrons.
Caractéristiques de la lumière diffractée
Interactions isotropes
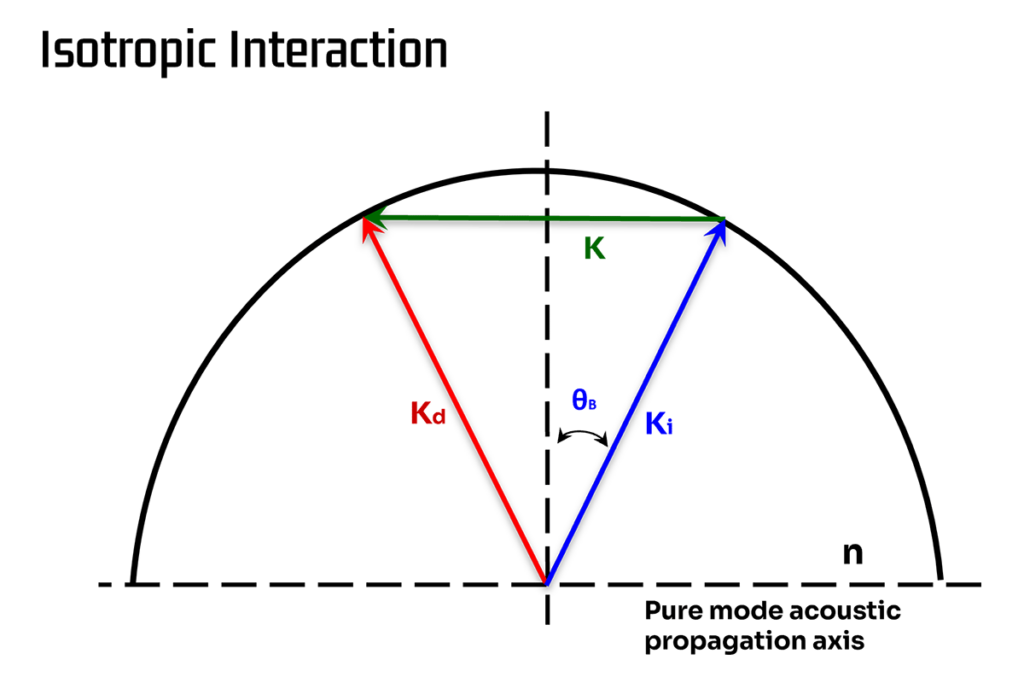
Une interaction isotrope est également appelée interaction en mode longitudinal. Dans ce cas, l’onde acoustique se propage longitudinalement dans le cristal et les faisceaux laser incident et diffracté ont le même indice de réfraction. Il s’agit d’une situation de grande symétrie et l’angle d’incidence correspond à l’angle de diffraction. Il n’y a pas de changement de polarisation associé à l’interaction.
Ces interactions se produisent généralement dans des cristaux homogènes ou dans des cristaux biréfringents coupés de manière appropriée.
Dans la situation isotrope, l’angle d’incidence de la lumière doit être égal à l’angle de Bragg, ⊖B:
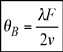
Où λ=λ0/n est la longueur d’onde à l’intérieur du cristal, v est la vitesse acoustique et F est la fréquence RF.
L’angle de séparation ⊖ entre les faisceaux de premier ordre et d’ordre zéro est le double de l’angle d’incidence et, par conséquent, le double de l’angle de Bragg.
L’intensité de la lumière diffractée I1 est directement contrôlée par la puissance acoustique P :

Ici I0 est l’intensité lumineuse incidente, M2 est le facteur de mérite acousto-optique du cristal et H et L sont la hauteur et la longueur du faisceau acoustique. λ0 est la longueur d’onde du faisceau incident.
L’efficacité de la diffraction (relative) est le rapport I1/I0:

Pour une orientation donnée, si la fréquence RF est légèrement différente de celle requise pour correspondre au critère de Bragg, la diffraction se produira toujours. Cependant, l’efficacité de la diffraction diminue. La situation est illustrée dans la figure ci-dessous, où le vecteur d’onde acoustique, K, est plus long que le vecteur d’onde, K0.
Une analyse compliquée conduit au résultat suivant :

Où ∆Φ = ∆K.L est appelé « asynchronisme de phase ».
![]()
Dans le cas isotrope :
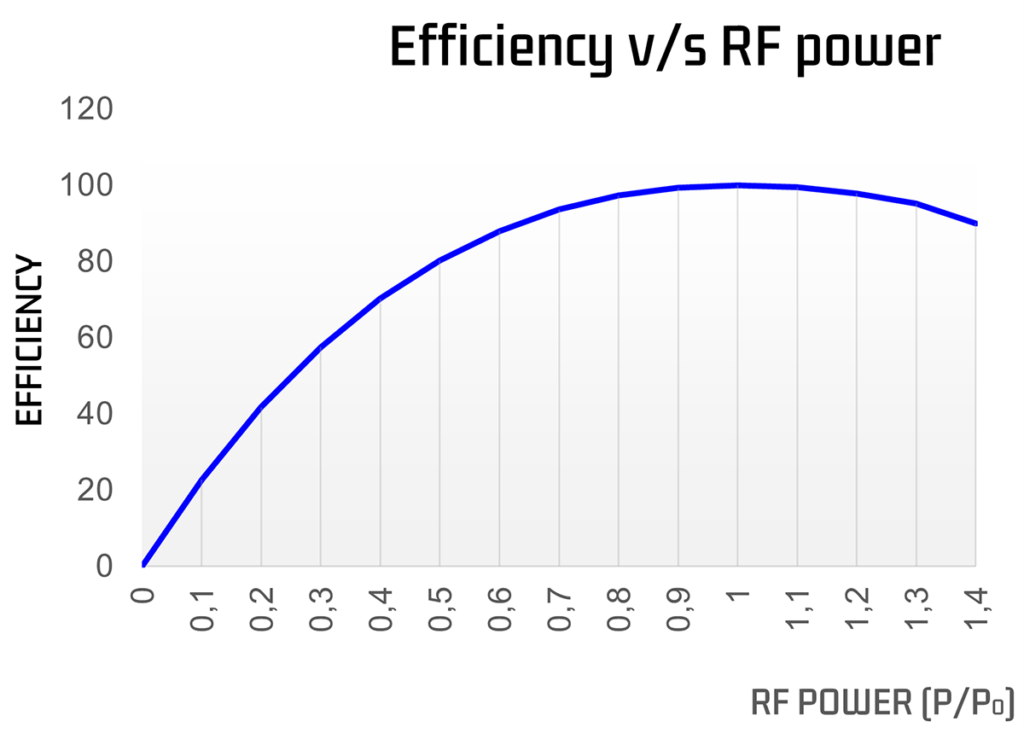
À la bonne fréquence de Bragg, (F=F0) l’efficacité est maximale.
Lorsque augmente, l’efficacité de la diffraction diminue et continuera à diminuer jusqu’à zéro.
S’il existe une limite inférieure à l’efficacité de diffraction acceptable, cela impose une limite à . Cela implique à son tour un maximum F et définit la largeur de bande RF du dispositif.
Pour augmenter cette largeur de bande RF, le rapport (la divergence acoustique) peut être augmenté. Lorsque la fréquence RF varie, la direction du faisceau diffracté change. C’est la raison d’être des déflecteurs acousto-optiques.
Interaction anisotrope
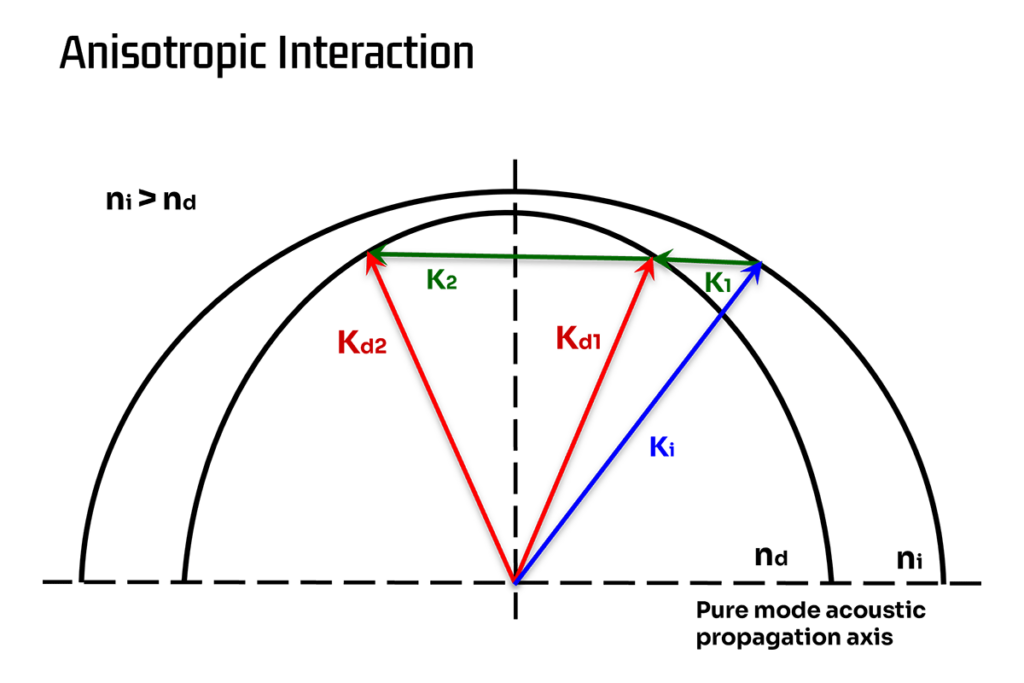
Dans une interaction anisotrope, en revanche, les indices de réfraction des faisceaux incident et diffracté seront différents en raison d’un changement de polarisation associé à l’interaction. Ceci est visible dans la figure ci-dessous où le vecteur d’onde acoustique relie les courbes d’indice de l’onde incidente et de l’onde diffractée. ( représente simplement une interaction similaire à une fréquence RF très différente).
La même asymétrie qui est à l’origine de la différence d’indices de réfraction entraîne également le déplacement de l’onde acoustique dans un « mode de cisaillement » et, dans l’exemple particulier du dioxyde de tellure (TeO2), cela se traduit par une réduction drastique de la vitesse acoustique.
Les interactions anisotropes offrent généralement une augmentation de l’efficacité et de la largeur de bande acoustique et optique. Elles sont utilisées presque universellement dans les dispositifs à grande ouverture. La réduction de la vitesse acoustique, observée dans le dioxyde de tellure en mode cisaillement, permet d’utiliser ce matériau dans des déflecteurs à haute résolution.
L’augmentation de la largeur de bande disponible dans les dispositifs à mode de cisaillement est illustrée de la manière la plus évidente dans la figure ci-dessous, où la configuration de l’interaction est choisie de manière à ce que le vecteur d’onde acoustique soit tangent à l’ellipse d’indice du faisceau diffracté.
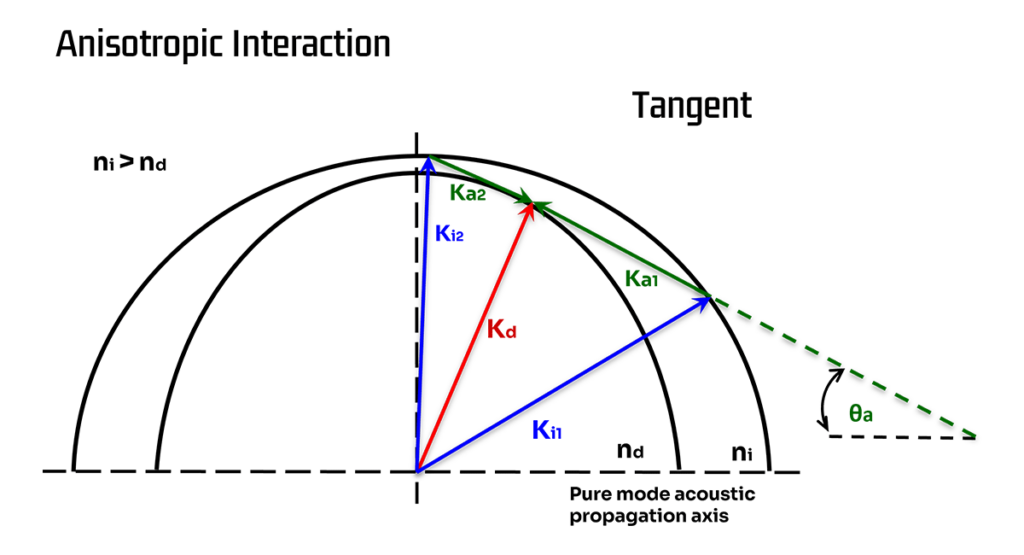
Cela signifie que la longueur du vecteur d’onde acoustique peut varier de manière assez importante tout en ne produisant que de faibles changements dans la longueur du vecteur d’onde du faisceau diffracté. Ainsi, dans cette situation, ∆K (and, hence, ∆Φ) est assez insensible aux changements de la fréquence RF.
Les interactions en mode de cisaillement sont beaucoup plus complexes à analyser et nécessitent des informations détaillées sur la coupe du cristal, les indices de réfraction et l’orientation. Cependant, ces interactions présentent de nombreux avantages et la plupart des déflecteurs et tous les AOTF utiliseront des interactions en mode cisaillement. La vitesse acoustique réduite rend ces dispositifs beaucoup plus lents que les unités à mode longitudinal, ce qui peut être considéré comme un inconvénient dans certaines circonstances.
